One Click Computation
One click computation and analysis for all load cases and modules
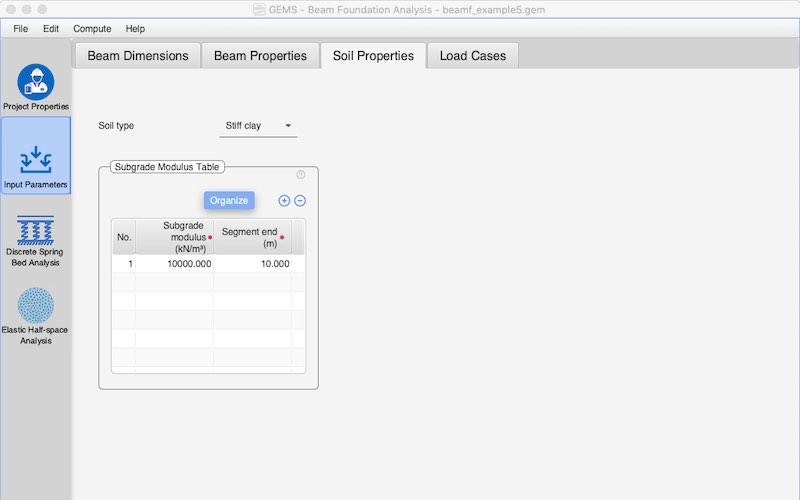
Beam foundation is adopted in the case of combined footing supporting two or more columns. The combined footing is modelled structurally as a beam foundation resting on the soil. The sub soil may be modelled in several ways. Two common models for the subsoil are:
(a) Discrete spring-bed model using modulus of subgrade reaction (also known as “beams on elastic foundation” or “Winkler beam theory”). The soil parameter used for this analysis is the modulus of subgrade reaction.
(b) Elastic half–space model where the subsoil model is replaced by elastic, homogeneous, isotropic semi-infinite continuum. The soil parameters used are elastic modulus and Poisson ratio.
The “Beam Foundations” software consists of two modules incorporating the above two commonly used models of analysis.This video details the design and analysis of a shallow foundation supporting a 3-storied building.
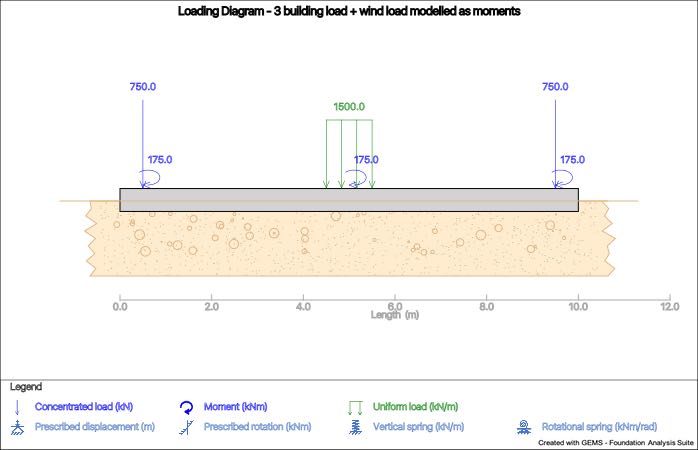
The dead load of the building is transferred to the beam foundation via columns and are modeled as concentrated loads.
GEMS Beam Foundation Analysis Software used in this video can be downloaded or accessed online from below links. It is advisable to try this in parallel along with the video.
One click computation and analysis for all load cases and modules
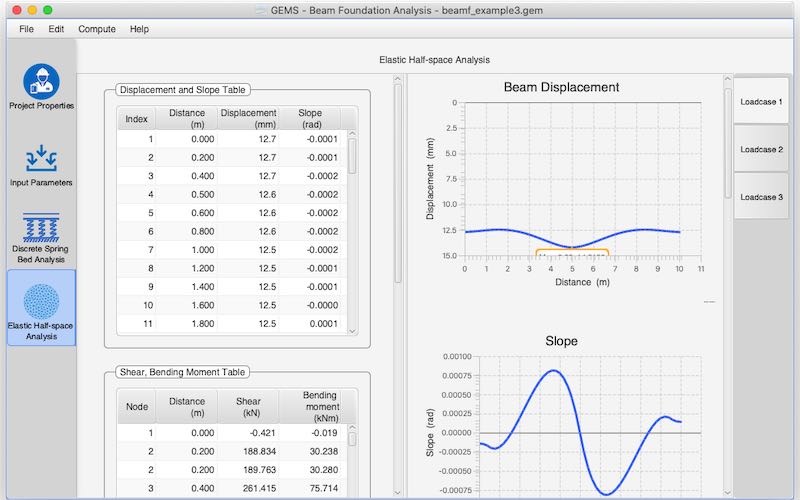
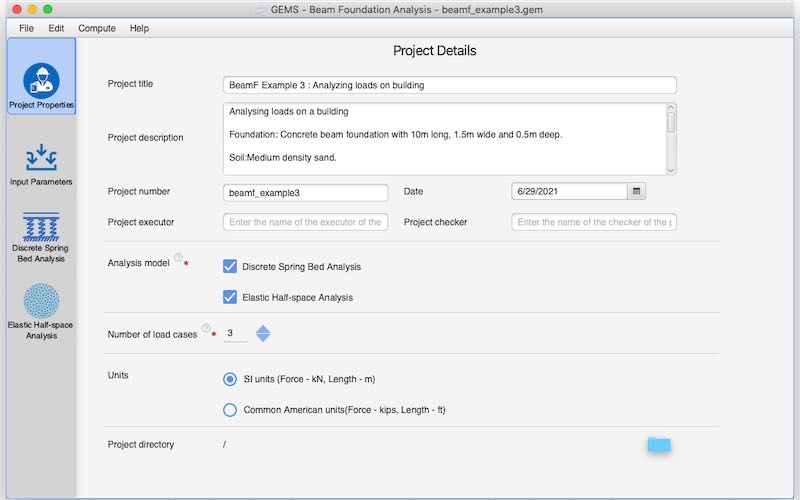
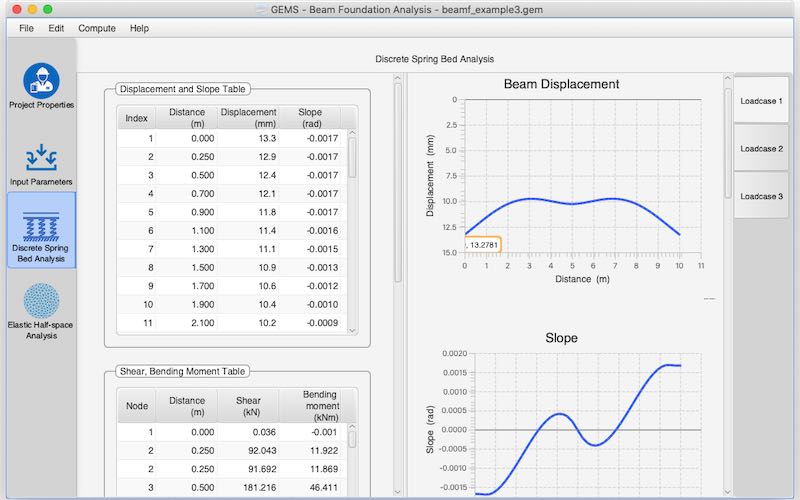
Analysis of the beam foundation using both/either models
Multiple load cases could be considered
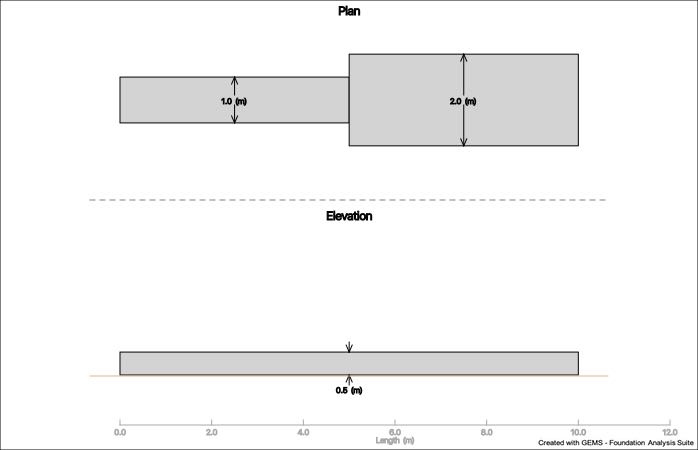
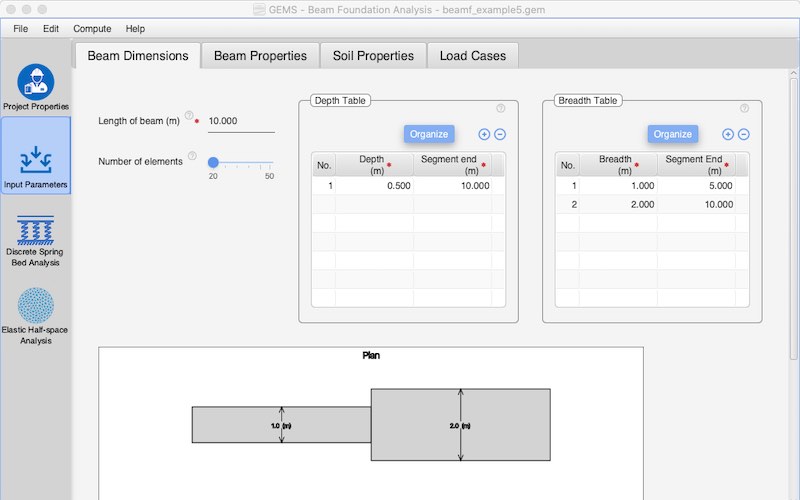
Graphical representation of the Plan and Elevation View of the beam foundation
Graphical representation of loading diagrams for each load case
Data can be input in either SI units or ‘Commonly used American units’ (Kips for force and foot for length)
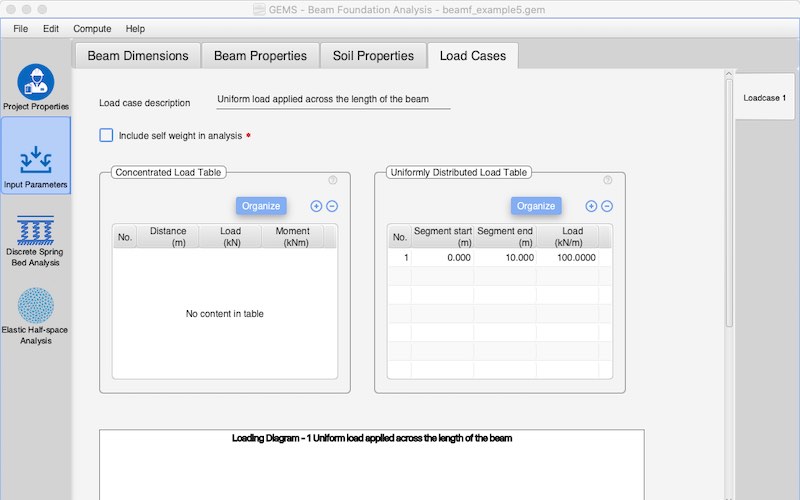
The loading may consist of several concentrated loads & moments
Multiple uniformly distributed loads can be specified
Self-weight of the beam may be included if required
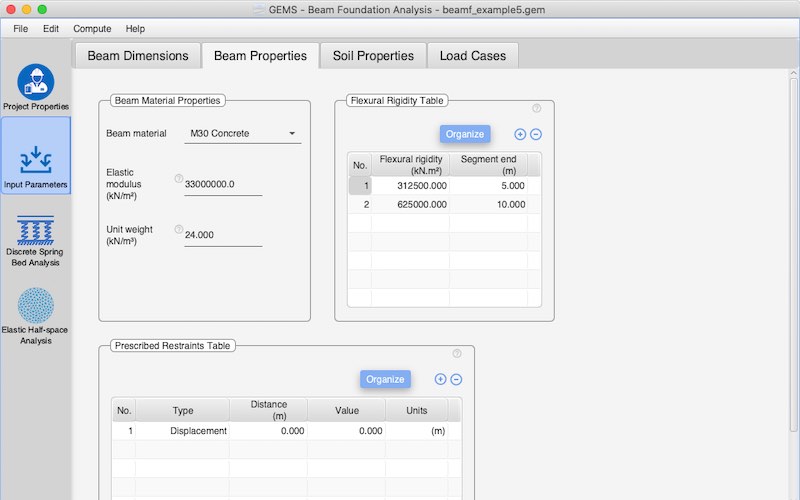
Different depths and breadths could be given for the beam. RCC inverted T beam sections and RSJ s could be considered by prescribing EI values directly
Vertical displacements and rotations could be prescribed if required
Export results to Microsoft Word, Excel & PDF
Support for Windows & Mac
Available on cloud using a browser
 Discrete
spring-bed model
Discrete
spring-bed model
This model is based on subgrade reaction
theory. The analysis of the foundation beam is based on the
solution of the differential equation
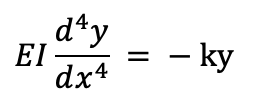 where k=k_s×B, EI=Flexural rigidity of foundation beam,
where k=k_s×B, EI=Flexural rigidity of foundation beam,
k_s=Modulus of subgrade reaction, B=width of foundation beam. The foundation base is assumed to be smooth and the soil pressure is assumed uniform across the width. The solution of this differential equation is complicated and cumbersome except for very simple problems. For practical problems where the loads are in the form of several concentrated loads, moments and UD loads it becomes necessary to resort to numerical solutions. The software module uses finite element solution of the problem using the exact displacement function and therefore gives exact solution to the problem.
 Elastic
half-space model
Elastic
half-space model
In this approach the subsoil is
modelled by a homogeneous, isotropic elastic half-space
characterised by an elastic modulus and a Poisson ratio. This
model has the merit of accounting for the continuous nature of
the soil medium. The discrete spring bed model does not account
for the soil continuity. The solution is based on the vertical
displacement due to a distributed surface loading on an elastic
half-space (given by “Boussinesq”). Again numerical solution of
the problem is essential for tackling practical problems as no
analytical solution is available for finite beams. The software
module for Elastic half-space model is based on finite element
formulation assuming a smooth base and uniform soil pressure
across the width.
Copyright © All Rights Reserved